Notes on "FFJORD: Free-form Continuous Dynamics for Scable Reversible Generative Models"
Abstract
T. Q. Chen等提出的连续时间可逆生成模型,在算法复杂度、内存效率、实践性能上都表现了很强的竞争力。
前言
可逆生成模型指通过变量转换将一个基分布变换为模型分布,并同时在单次传播中保持高效密度估计与采样能力的模型。目前这类工作包括Dinh等的NICE(ICLR2014),Dinh等的Real NVP(ICLR2017)以及Kingma等的Glow.
这些方法拥有一些以往生成模型不具备的特点,但同时由于训练算法较高的复杂度,通常要进行结构或者参量上的限制。这篇文章基于T. Q. Chen 2018年所提出的基于微分方程连续时间形式的标准化流,将其中利用迹进行似然计算的方法进一步改进,引入一个似然的无偏随机估计器用于降低算法复杂性,最终能够以 \(\mathcal{O}(D)\) 的代价进行训练,使得可逆生成模型可以使用任意的网络结构。
可逆生成模型
相比直接参数化一个标准化分布,变量替换公式允许我们通过一个可逆的函数\(f : \mathbb{R}^{D} \rightarrow \mathbb{R}^{D}\)将基分布 \(p_{\mathbf{z}}(\mathrm{z})\) 进行变换,隐式地表示一个复杂的标准化分布。给定一个随机变量\(\mathbf{z} \sim p_{\mathbf{z}}(\mathbf{Z})\),则\(\mathrm{x}=f(\mathrm{z})\)的对数密度满足: \[ \log p_{\mathbf{x}}(\mathbf{x})=\log p_{\mathbf{z}}(\mathbf{z})-\log \operatorname{det}\left|\frac{\partial f(\mathbf{z})}{\partial \mathbf{z}}\right|\tag{1.1} \] 这里\(\partial f(\mathbf{z}) / \partial \mathbf{z}\)是\(f\)的雅克比阵。一般而言,对式子\((1.1)\)中对数行列式的计算需要\(\mathcal{O}(D^3)\)的时间复杂度,这使得此类方法通常需要限制神经网络的结构,以降低计算代价,可以分为以下三类:
- 标准化流.通过限制\(f\)的函数形式,可以得到很多行列式的一致性。由于没有解析形式的\(f^{-1}\),这类模型不能直接在数据上训练以及进行采样,但在表示用于变分推断的近似先验时是有效的。
- 自回归变换.通过使用自回归模型并固定维度上的顺序,\(f\)的雅克比阵被转变为下三角型。这类模型擅长于表格式数据的密度估计,但是需要\(D\)个\(f\)的序列估计用于逆变换,当维度较大时难以进行。
- 分割式变换.对维度进行分割并使用仿射变换使得雅克比阵行列式计算十分简单,并且\(f^{-1}\)的计算代价与\(f\)相同。这允许了卷积结构的使用,在图像数据的密度估计上十分有效。
连续标准化流
在2018年T.Q.Chen等提出了类似基于式子\((1.1)\)方法的生成式模型,它将变换函数替换为连续时间动力系统的积分。首先从基分布\(\mathbf{z}_{0} \sim p_{z_{0}}\left(\mathbf{z}_{0}\right)\)中采样,然后给定一个由参量函数\(f(\mathbf{z}(t), t ; \theta)\)确定的微分方程,求解初值问题\(\mathbf{z}\left(t_{0}\right)=\mathbf{z}_{0},\partial z(t) / \partial t=f(\mathbf{z}(t), t ; \theta)\)得到\(\mathbf{z}(t_1)\)即构成了可见数据. 在这个模型下对数密度满足第二个微分方程,称为瞬时变量变换公式: \[ \frac{\partial \log p(\mathbf{z}(t))}{\partial t}=-\operatorname{Tr}\left(\frac{\partial f}{\partial \mathbf{z}(t)}\right)\tag{1.2} \] 在时间上积分,即可计算对数密度的整个变化: \[ \log p\left(\mathbf{z}\left(t_{1}\right)\right)=\log p\left(\mathbf{z}\left(t_{0}\right)\right)-\int_{t_{0}}^{t_{1}} \operatorname{Tr}\left(\frac{\partial f}{\partial \mathbf{z}(t)}\right) d t\tag{1.3} \]
给定一个数据点\(\mathbf{x}\),我们可以同时计算它原像\(\mathbf{z}_0\),以及在模型下\(\mathbf{x}\)的对数概率密度: \[ \left[ \begin{array}{c}{\mathbf{z}_{0}} \\ {\log p(\mathbf{x})-\log p_{z_{0}}\left(\mathbf{z}_{0}\right)}\end{array}\right]=\int_{t_{1}}^{t_{0}} \left[ \begin{array}{c}{f(\mathbf{z}(t), t ; \theta)} \\ {-\operatorname{Tr}\left(\frac{\partial f}{\partial \mathbf{z}(t)}\right)}\end{array}\right] d t,\left[ \begin{array}{c}{\mathbf{z}\left(t_{1}\right)} \\ {\log p(\mathbf{x})-\log p\left(\mathbf{z}\left(t_{1}\right)\right)}\end{array}\right]=\left[ \begin{array}{l}{\mathbf{x}} \\ {0}\end{array}\right]\tag{1.4} \] 它对\(z(t)\)与样本的对数密度组合成的动力系统从\(t_1\)到\(t_0\)后向积分。式子\((1.4)\)的存在与唯一性需要\(f\)和其一阶导数都是Lipschitz连续的,这只要在神经网络中使用光滑Lipschitz激活函数即可。
使用ASM进行反向传播
CNF使用极大似然进行训练,即最大化式子\((1.3)\)。这个目标函数包含了以\(\theta\)为参数的初值问题的解,而解是没有解析形式的,梯度的求解成为了一个阻碍。实际上,对于任意的度量函数: \[ L\left(\mathbf{z}\left(t_{1}\right)\right)=L\left(\int_{t_{0}}^{t_{1}} f(\mathbf{z}(t), t ; \theta) d t\right)\tag{1.5} \] adjoint state method都能够通过解一个伴随微分方程,求出泛函对参量的梯度: \[ \frac{d L}{d \theta}=-\int_{t_{1}}^{t_{0}}\left(\frac{\partial L}{\partial \mathbf{z}(t)}\right)^{T} \frac{\partial f(\mathbf{z}(t), t ; \theta)}{\partial \theta} d t\tag{1.6} \] 而求解时是从时刻\(t_1\)后向进行的,即最终的推断结果,这是反向传播的连续推广,具体的流程可以参考T.Q.Chen等在neurips2018上的文章。
使用任意网络结构进行定量密度估计
CNF将标准化流进行了连续化处理,这使得算法的复杂度从\(\mathcal{O}\left(D^{3}\right)\)降低到了\(\mathcal{O}\left(D^{2}\right)\),使得我们能够选择更复杂的模型。这篇文章作为后续工作,将算法时间复杂度进一步降低,对网络结构的限制被极大降低。
无偏线性时间对数密度估计
计算\(\operatorname{Tr}(\partial f / \partial \mathbf{z}(t))\)的时间复杂度为\(\mathcal{O}\left(D^{2}\right)\),由于雅克比阵对角线上的每个量都需要求解一个独立的\(f\)的微分,有两种方式可以降低复杂度。首先,使用反向自动微分,向量-雅克比阵积\(\boldsymbol{v}^T\frac{\partial f}{\partial \boldsymbol{z}}\)可以用近似计算\(f\)的代价得到。第二,我们可以使用一个噪声向量的权平方进行矩阵迹的无偏估计: \[ \operatorname{Tr}(A)=E_{p(\boldsymbol{\epsilon})}\left[\boldsymbol{\epsilon}^{T} A \epsilon\right]\tag{2.1} \] 上面的等式对于任意\(D^2\)矩阵\(A\)以及满足\(\mathbb{E}[\epsilon]=0\)和\(\operatorname{Cov}(\boldsymbol{\epsilon})=I\)的\(D\)维随机向量\(\boldsymbol{\epsilon}\)都成立,使用式\((2.1)\)的蒙特卡洛估计称为Hutchinson迹估计。
为了保持每次调用ODE solver时动力系统的确定性,这里在每次求解时都使用固定的\(\boldsymbol{\epsilon}\): \[ \begin{aligned} \log p\left(\mathbf{z}\left(t_{1}\right)\right) &=\log p\left(\mathbf{z}\left(t_{0}\right)\right)-\int_{t_{0}}^{t_{1}} \operatorname{Tr}\left(\frac{\partial f}{\partial \mathbf{z}(t)}\right) d t \\ &=\log p\left(\mathbf{z}\left(t_{0}\right)\right)-\int_{t_{0}}^{t_{1}} \mathbb{E}_{p(\boldsymbol{\epsilon})}\left[\boldsymbol{\epsilon}^{T} \frac{\partial f}{\partial \mathbf{z}(t)} \boldsymbol{\epsilon}\right] d t \\ &=\log p\left(\mathbf{z}\left(t_{0}\right)\right)-\mathbb{E}_{p(\boldsymbol{\epsilon})}\left[\int_{t_{0}}^{t_{1}} \epsilon^{T} \frac{\partial f}{\partial \mathbf{z}(t)} \epsilon d t\right] \end{aligned}\tag{2.2} \] 通常从标准正态分布或者Rademacher分布采样\(\boldsymbol{\epsilon}\),上面的改进使得时间复杂度降为\(\mathcal{O}\left(D\right)\).
使用Bottleneck增强稳定性
Bottleneck即隐藏层的宽度\(H\)比输入维度\(D\)更小,通过迹的循环对称性我们可以使Hutchinson迹估计更加稳定。这是因为Hutchinson迹估计的方差以渐进\(||A||_F^2\)增长,因此降低维度应该对减少方差有帮助。将动力项视作两个函数的复合\(f=g \circ h(\mathbf{z})\),那么有: \[ \operatorname{Tr} \underbrace{\left(\frac{\partial f}{\partial \mathrm{z}}\right)}_{D \times D}=\operatorname{Tr} \underbrace{\left(\frac{\partial g}{\partial h} \frac{\partial h}{\partial \mathrm{z}}\right)}_{D \times D}=\operatorname{Tr} \underbrace{\left(\frac{\partial h}{\partial \mathrm{z}} \frac{\partial g}{\partial h}\right)}_{H \times H}=\mathbb{E}_{p(\boldsymbol{\epsilon})}\left[\epsilon^{T} \frac{\partial h}{\partial \mathbf{z}} \frac{\partial g}{\partial h} \epsilon\right]\tag{2.3} \] 当\(f\)含有多个层时,选择\(H\)为最小维度。
FFJORD
使用FFJORD进行对数密度估计算法如下

实验
这里只展示密度估计的对比实验:
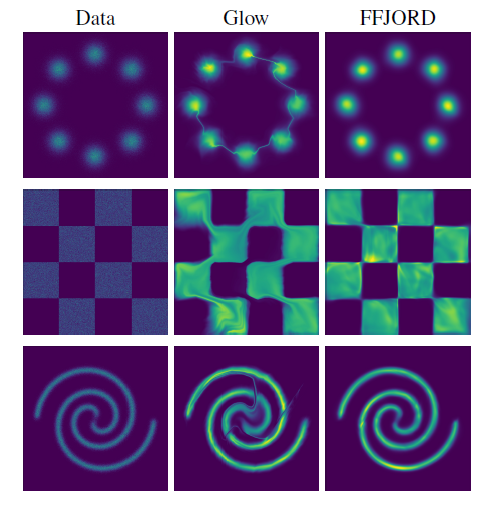
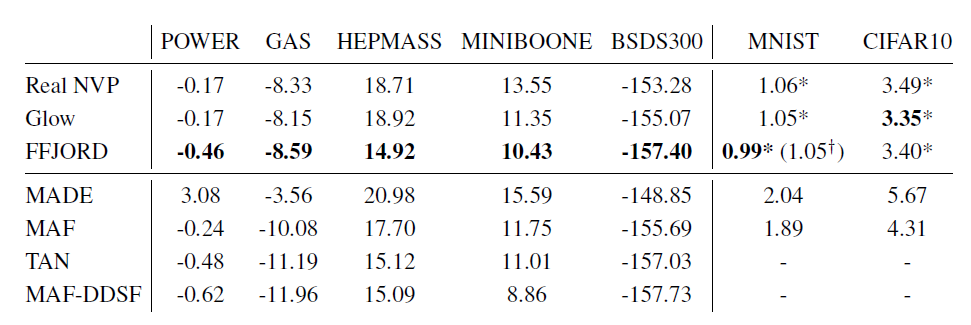
Glow在模型化分离区域中间的低概率部分时出现了问题,如第一张图所示。在MNIST上,FFJORD使用单个流就可以达到Glow和Real NVP的效果,当使用多尺度流时达到了更好的效果,并且其参数量不到Glow的2%. FFJORD相比最好的方法更慢,但asm的高内存效率使得它能每次在多得多的数据上优化。
使用VAE进行变分推断的对比实验也表明FFJORD的性能更加优越,这里省略。