最近一些工作研究了GNN的预训练,但是关于GNN的可迁移性并没有理论根据。这篇文章建立了一个有理论保证的图神经网络迁移学习框架。框架包含两个部分,第一是Ego-graph information maximization(EGI)的迁移方法,第二是当节点特征是结构相关时分析了EGI的可迁移性。
动机和贡献
尽管有不少关于GNNs可迁移性的工作:
- Strategies for pre-training GNNs ICLR19
- Gpt-gnn: Generative pre-training of GNNs KDD20
- Pre-training GNNs for generic structural feature extraction
- Node classification on graphs with few-shot novel labels via meta transformed network embedding NIPS2020
- Learning to extrapolate knowledge: Transductive few-shot out-of-graph link predictionNIPS2020
- Graphon neural networks and the transferability of GNNsNIPS2020
- Shift-robust gnns: Overcoming the limitations of localized graph training dataNIPS2020
但是对什么情况下这种迁移(预训练+微调)会失效,并没有很好的探究清楚。这篇文章就基于domain adaptation的框架,直接研究源域到目标域的迁移问题,来进行可迁移性的理论分析。
可迁移GNNs
GNN的表示能力应该是对节点特征和拓扑结构的联合分布的建模能力,那么可迁移性实际上是模型对两个域分布的建模能力的差距。如果在模型的表示下,这两个分布差距并不是很大,那么迁移就是可能的。
基于EGI的可迁移GNN
这篇文章研究GNN的直接迁移,即在源域做预训练,然后在目标域不进行微调进行预测。直观上来说,\(G_a,G_b\)需要有相似之处,这种直接迁移才是有可能的。我们首先给出K-hop ego-graph的定义。
定义3.1(K-hop ego-graph)称\(g_i=\{V(g_i),E(g_i)\}\)为一个以\(v_i\)节点为中心的k-hop eog-graph,如果它有一个k层质心展开,使得\(v_i\)和ego-graph其余节点的最大距离为\(k\)。在这里,对于以\(\hat{v}_c\)为质心的图\(G(V,E)\),它的K层质心展开子图\(\mathcal{G}_{K}(\mathcal{V}_K;\mathcal{E}_K)\)是:
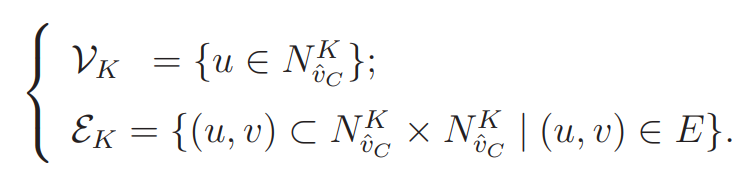
\(N_{\hat{v}_C}^K=\{u\in V|S_{G}(\hat{v}_C,u)\le K\}\),\(S_G(u,v)\)是\(u,v\)最短路径的长度。实际上就是以\(\hat{v}_C\)为中心,最短路径小于等于\(K\)的节点构成的子图。
定义3.2(Structural information)令\(\mathcal{G}\)为子图的拓扑空间,我们将图\(G\)视为从k-hop ego-graphs\(\{g_i\}_{i=1}^n\)中i.i.d采样的结果。\(G\)的结构信息由k-hop ego-graphs以及对应的经验分布定义。
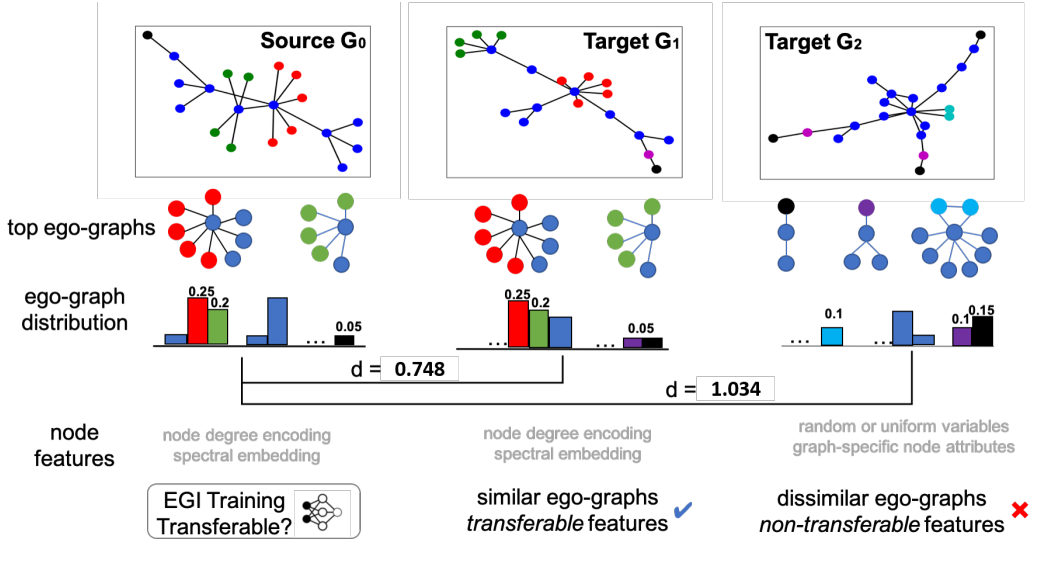
这篇文章基于k-hop subgraph kernel,将graph视为从k-hop ego-graph structure和节点feature中采样的结果。然而,现有的任务无法对ego-graph的分布进行建模。这边文章提出了EGI去使用互信息最大化来重构k-hop ego-graph。在Figure 1中,作者展示了\(G_0,G_1,G_2\)的k-hop ego-graph。在实际情况中,除了k-hop ego-graph,图还包含了节点特征,因此\(G\)应该视为两者联合分布的采样。
EGI.给定一个从分布\((g_i,x_i)\sim\mathbb{P}\)中采样出的ego-graphs的集合\(\{(g_i,x_i)\}\)。这篇文章希望训练编码器\(\Psi\)来最大化\(MI(g_i,\Psi(g_i,x_i))\),即节点表示\(z_i=\Psi(g_i,x_i))\)和结构信息的互信息。为了最大化MI,判别器\(D(g_i,z_i)\)被用来计算边\(e\)属于\(g_i\)的概率。最终,作者使用Jensen-Shannon MI估计来做优化: \[ \mathcal{L}_{EGI}=-\text{MI}^{(JSD)}(\mathcal{G},\Psi)=\frac{1}{N}\Sigma_{i=1}^N[sp(\mathcal{D}(g_i,z_i'))+sp(-\mathcal{D}(g_i,z_i))] \] \(sp(x)=\log(1+e^x)\),\((g_i,z_i')\)由边际分布产生,即\(z_i'=\Psi(g_{i'},x_{i'}),(g_{i'},x_{i'})\sim\mathbb{P}\)。虽然作者说负样本也可以随机产生,但我估计这样做效果会很差。
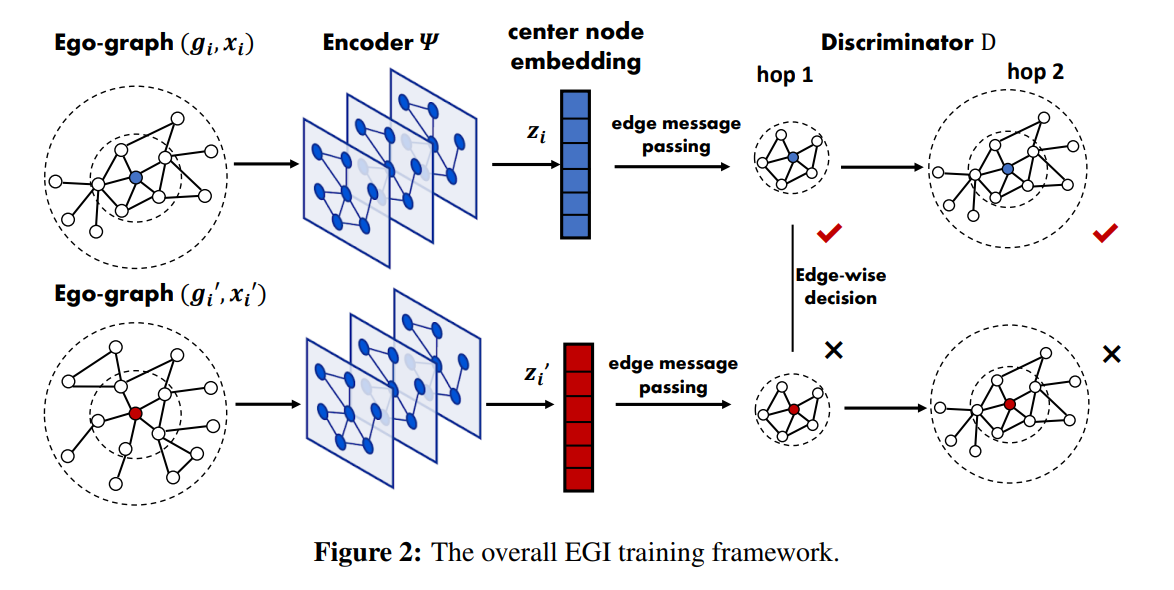
在判别器的计算时,它取决于节点顺序。这里作者采取了图生成的常见trick,使用混合顺序,即边集\(E(g_i)\)的广度优先顺序\(\pi\)。\(\mathcal{D}=f\circ\Phi\),\(\Phi\)是另外一个编码器,\(f\)是按照边序列\(E^{\pi}:\{e_1,e_2,\dots,e_n\}\)的评分函数。
我们直接来看这个评分函数,对于任意一对节点\((p,q)\in E^{\pi}\),\(h_p\)是由\(\Phi\)产生的source node的表示,\(x_q\)是target node的节点特征,评分函数如下: \[ f(h_p,x_q,z_i)=\sigma(U^T\cdot \tau(W^T[h_p||x_q||z_i])) \] 判别器\(\mathcal{D}\)被要求去区分正负样本\(((p,q),z_i),((p,q),z_i')\),按照\(g_i\)的BFS顺序。\((p,q)\)有两种类型,第一种是穿过了不同hop的,第二种是同一hop之中的。由于我们使用的是BFS顺序,所以对第二种不敏感。其次对于两个编码器\(\Psi,\Phi\),其输入都只需要一个k-hop ego-graph,因此只要对\(g_i\)采样,就可以进行并行训练。只要\((g_i,x_i)\)在两个域都满足3.2节给出的条件,EGI就是可迁移的。(这一段的写作真的太迷了。。。搞不懂写这么烂怎么不被challenge的。)
与现有工作的关联 上面的互信息最大化,其对偶问题实际上是一个重构问题。 \[ \max \text{MI}(g_i,x_i)=H(g_i)-H(g_i|\Psi(g_i,x_i))\le H(g_i)-R(g_i|\Psi(g_i,x_i)) \] 从这个角度,EGI和VGAE的区别在于VGAE假设每条边都是被独立输入的,而EGI是同时作为输入的。现有基于互信息的方法比如DGI和GMI更关注节点特征,而图结构对于迁移性是更重要的。
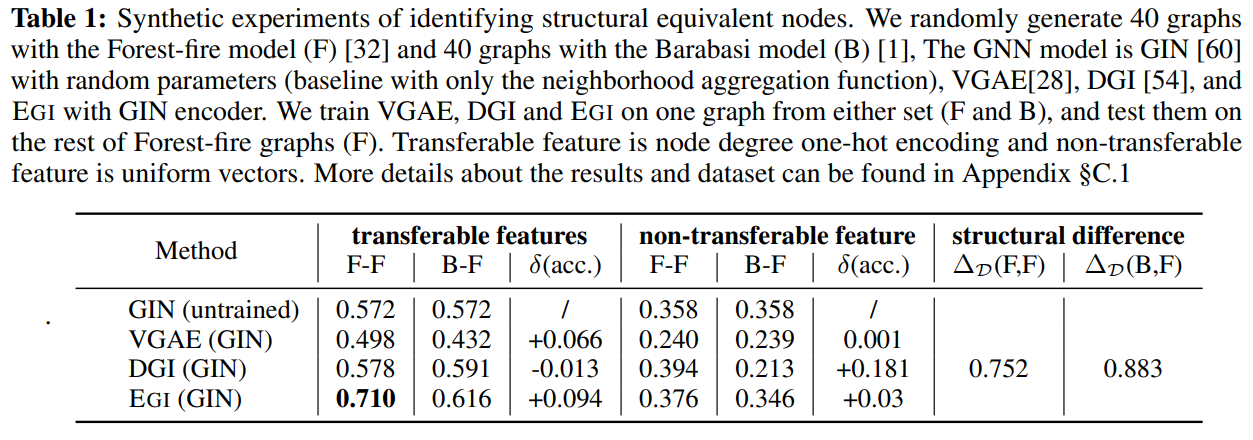
支持性的观察(这些东西到底是哪个会议的格式。。我好像没见过这么写的)Table 1展示了迁移的结果。
基于局部graph lapalcians的可迁移性分析
我们首先给出以下的定义。
定义3.3(Structure-respecting node features).令\(g_i\)为以\(v_i\)为中心的有序ego-graph,其节点特征为\(\{x_{p,q}^i\}_{p=0,q=1}^{k,|V_p(g_i)|}\),\(V_p(g_i)\)是\(g_i\)的p阶领域节点。如果\(x_{p,q}^{i}=[f(g_i)]_{p,q}\in\mathbb{R}^d\)对于任意节点\(v_q\in V_p(g_i)\),\(f:\mathcal{G}\to\mathbb{R}^{d\times |V(g_i)|}\)成立,那么就说这个节点特征是结构相关的。
这个定义其实跟图信号处理的差不多。他这个文章从头到尾都在强调他的theorem3.1,但是又不说具体内容,theorem3.1又放到很后面,读起来真的很痛苦。写作一定要避免这种问题。我们直接来看他的theorem3.1说了什么吧。
定理3.1(GNN transferablity).令\(G_a=\{(g_i,x_i)\}_{i=1}^n\),\(G_b=\{(g_{i'},x_{i'})\}_{i'=1}^m\)为两个图,假设它的节点特征是结构相关的。考虑GCN\(\Psi_{\theta}\)有k层,每层一个1-hop polynomial filter \(\phi\)。只要\(G_a\)和\(G_b\)的局部谱满足一定条件,那么有下面的估计成立: \[ |\mathcal{L}_{EGI}(G_a)-\mathcal{L}_{EGI}(G_b)|\le\mathcal{O}(\Delta_\mathcal{D}(G_a,G_b)+C) \] \(C\)仅取决于图编码器和节点特征,\(\Delta_\mathcal{D}(G_a,G_b)\)衡量了两者结构差距 \[ \Delta_\mathcal{D}(G_a,G_b)=\tilde{C}\frac{1}{nm}\Sigma_{i=1}^n\Sigma_{i'=1}^m\lambda_{max}(\tilde{L}_{g_i}-\tilde{L}_{g_{i'}}) \] \(\tilde{C}\)是一个常数,取决于源域laplacian的最大特征值以及判别器。
定理3.1有个两个用途,用于EGI预训练的point-wise pre-judge和pair-wise pre-selection。假设我们有一个目标图\(G_b\),没有充足的训练标签。我们可以用结构差距去从有充足标签的\(G_a\)中筛选合适的pair,以提升\(G_b\)上的性能。对于计算效率的问题,作者说我们可以通过采样去估计这个GAP,并给出了实验结果。
我认为他方法的主要问题在于没有考虑标签,当两张图的异质性完全不同时,这种迁移也是不可能的。比如源域中同一邻域的节点大多都被归为一类,而目标域图上的异质性很强。这个时候做迁移就比较困难:对于源域,节点应该被分为邻域中占多数的。对于目标域,节点则不应该被分为占多数的。
实验
Airport包含三个图,来自三个不同的地方。节点是一个机场,边是航班。[Gene](https://proceedings.neurips.cc/paper/2019/file/e57c6b956a6521b28495f2886ca0977a-Paper.pdf包含50种癌症的基因交互。每个基因都包含一个标签,表明它是否是转录因子。
对于airport,作者在europe上训练,然后在三个数据集上测试。
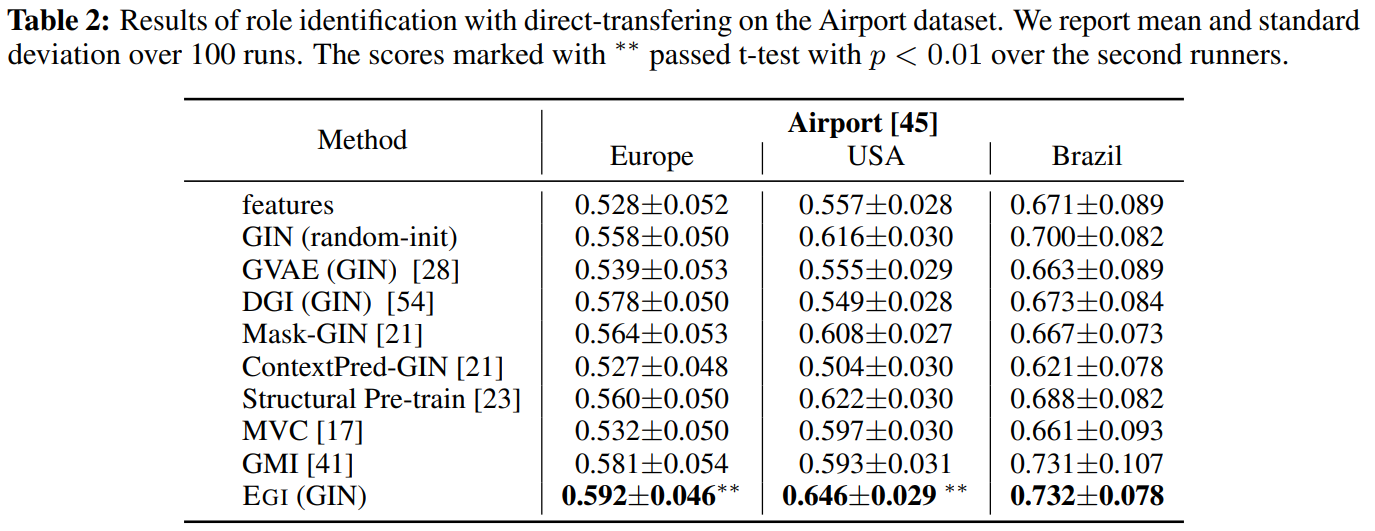
对于Gene,作者在一张图上训练,然后在另一张图上测试。FIgure3种,横轴显示了GAP,纵轴显示了精度提升。

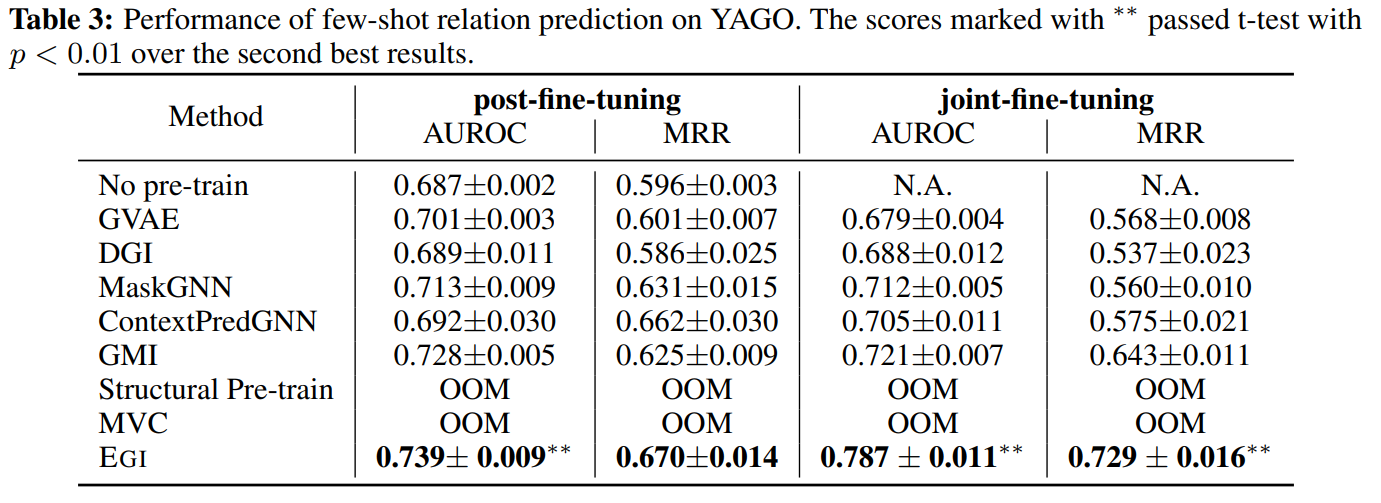
作者还在YAGO上进行了少样本学习的实验,在post-fine-tuning中,模型被无监督地预训练,然后再目标图上做微调。在joint-fine-tuning中,两部分损失被同时优化。
结语
总的来说,这篇文章良好地定义了图的迁移学习问题,把图数据本身视作ego-graph和特征的联合分布的采样。然后从这个角度去考虑直接迁移问题,即不做微调的迁移学习。个人认为,他考虑到了很关键的问题,即图数据的特殊之处。但是另一方面,这样的采样真的能够重构出原本的图数据吗?以及,标签信息为什么对迁移完全没有影响?这些都是这篇文章的漏洞。
这篇文章的写作也称不上是清晰简洁,作为文章的理论支撑,theorem3.1的内容完全没有被提前概括,以至于看前面的内容会非常困惑。这个文章另一点让我最困惑的就是评分函数那部分,为什么要用\(x_q\)?以及边的遍历顺序为什么会对结果有影响?他这部分本应该写得更加清楚,把这些为什么都说明白,但全都一句话带过了。