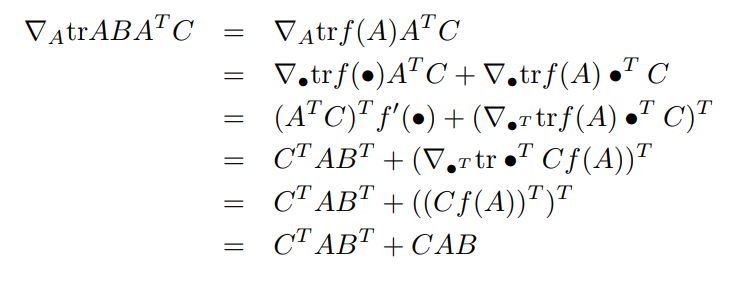Matrix Calculus
对于矩阵函数,我们也有对应的求导法则,这些法则对于矩阵的优化是必要的,掌握它们便于我们进行实际应用中的数值分析。对于\(n\times n\)矩阵,以及\(n\times 1\)的向量:

一些例子
我们先从一些简单的函数开始,假设:
\[ E=\mathrm{x}^T\mathrm{x} \]
\(E\)是一个标量函数,\(E\)对\(\mathrm{x}\)求导的结果应该是一个和\(\mathrm{x}\)同样形状的向量。经过简单的运算,我们有:
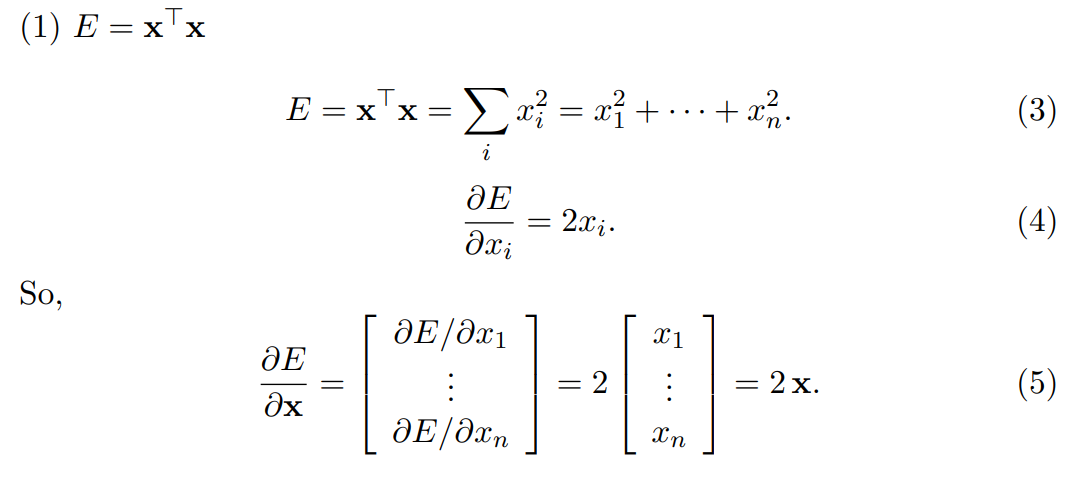
假设:
\[ E=\mathrm{x}^T\mathrm{y} \]
这和上面的是同样情况,\(E\)关于\(\mathrm{x}\)求导结果也是一个向量。
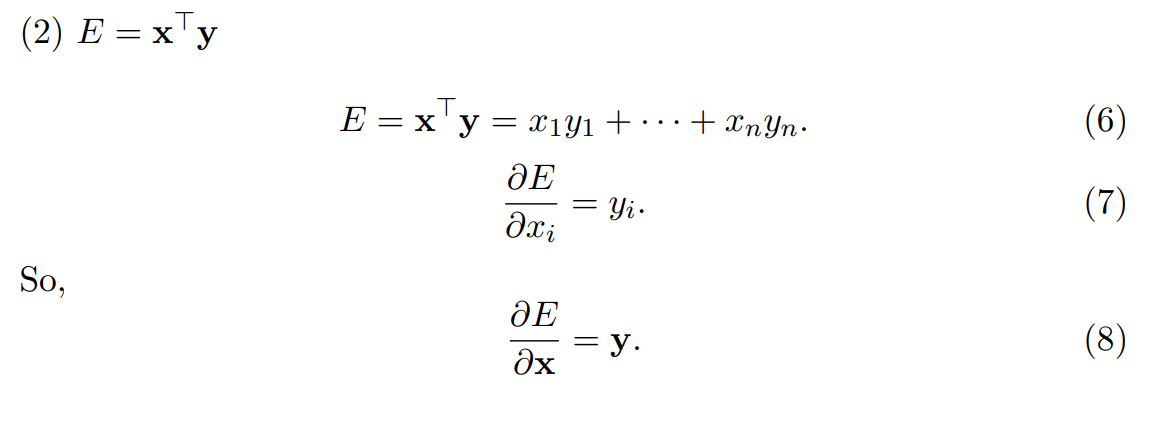
最后一个例子可以看出链式法则在矩阵求导时是怎么起作用的,假设:
\[ E=(\mathrm{x}^T\mathrm{y})^2 \]
对\(\mathrm{x}\)求导的话,结果应该是一个向量,按照链式法则:
\[ \frac{\partial E}{\partial \mathbf{x}}=\frac{\partial E}{\partial f}\frac{\partial f}{\partial \mathbf{x}} \]
这种链式法则根据求导的类型,会有形式上的变化,比如左乘或者右乘。避免不出错的方式是检查运算是否合法,以及结果的形状是否正确。比如两个\(n\times 1\)的向量就不能直接乘,求导结果肯定是把其中一个转置。经过这种检查后,基本上是不会出错的。对于上面的函数,我们有:
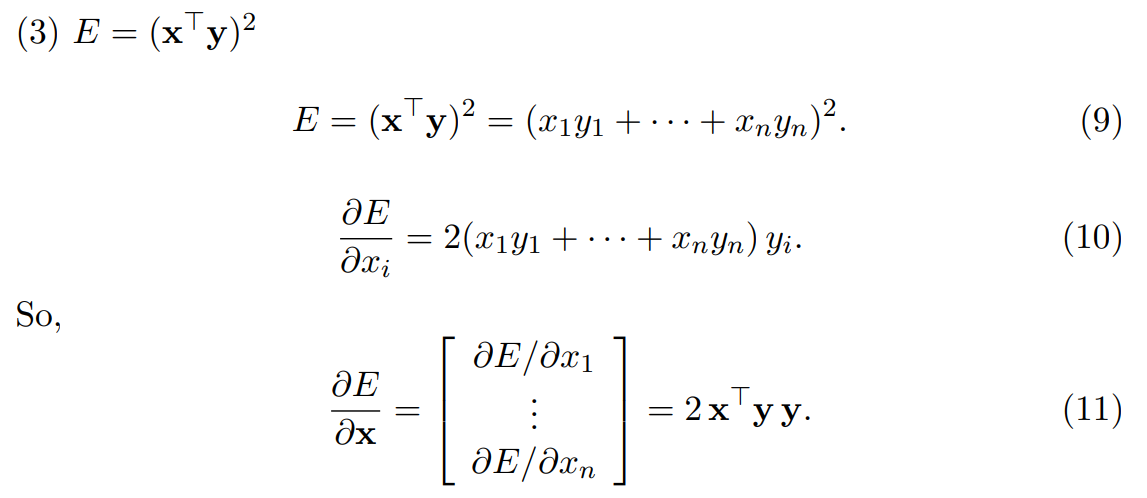
链式法则仍然是成立的。
下面我们来看含有矩阵的情况,即对\(\mathbf{Ax}\)进行求导。由于\(\mathbf{Ax}\)的结果是一个向量,对向量\(\mathbf{x}\)的求导结果是一个矩阵:
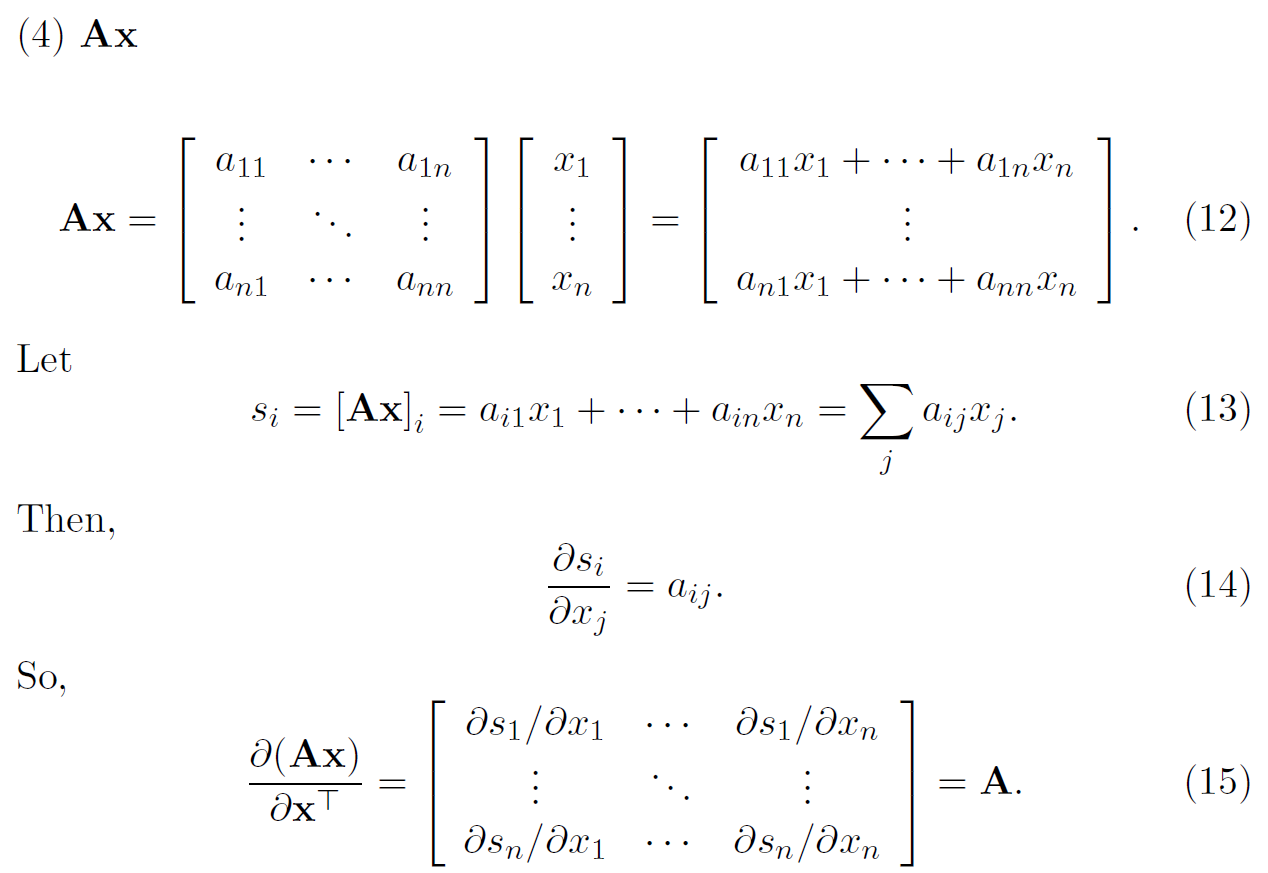
\(\mathbf{Ax}\)是\(n\times 1\)向量,所以应该对\(\mathbf{x}^T\in \mathbb{R}^{1\times n}\)求导,即沿着另外一条轴求导,得到一个\(n\times n\)向量。类似地,我们可以得到\(\frac{\partial(\mathbf{Ax})^T}{\partial \mathbf{x}}=\mathbf{A}^T\),根据定义可以验证这个结果。
应用中最常见的是处理含有范数的优化,假设:
\[ E=||\mathbf{Ax}||^2 \]
\(E\)是标量,如果对\(\mathbf{x}\)求导,得到的是一个向量。
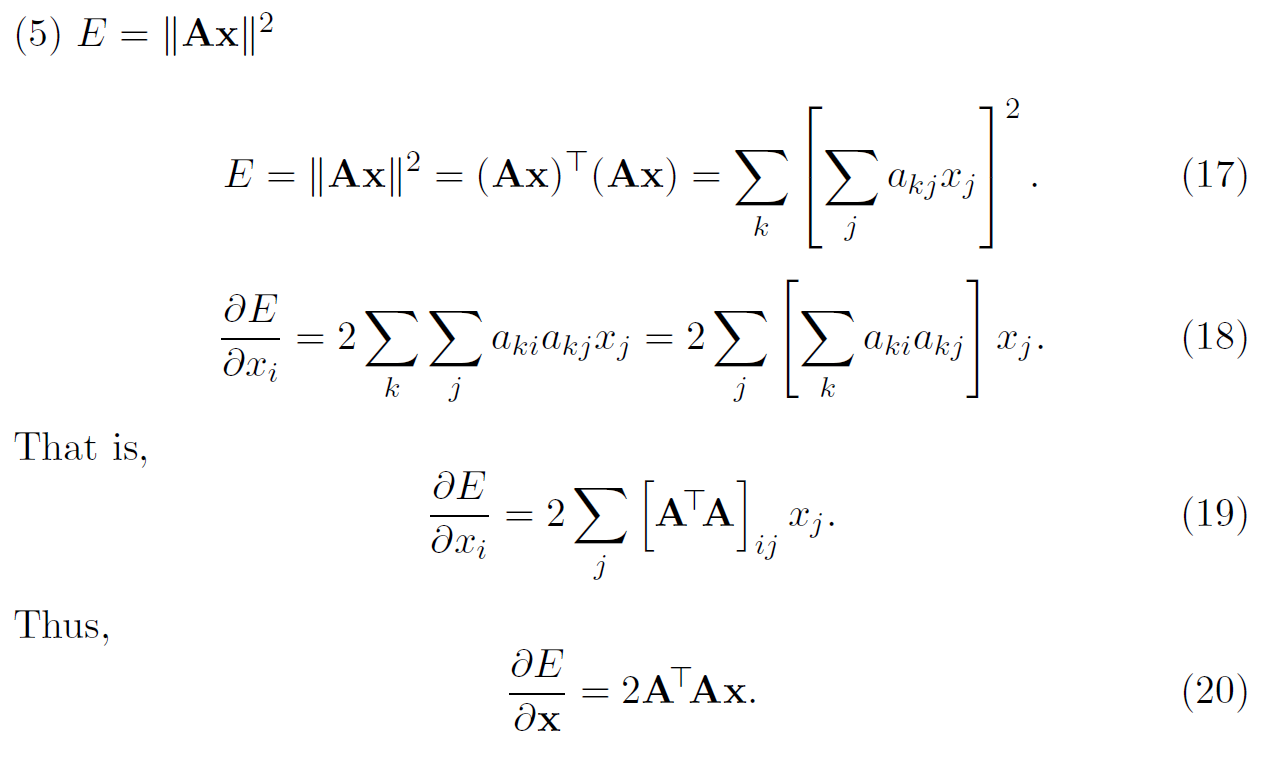
如果是对\(\mathbf{A}\)求导,那么得到的是一个矩阵。
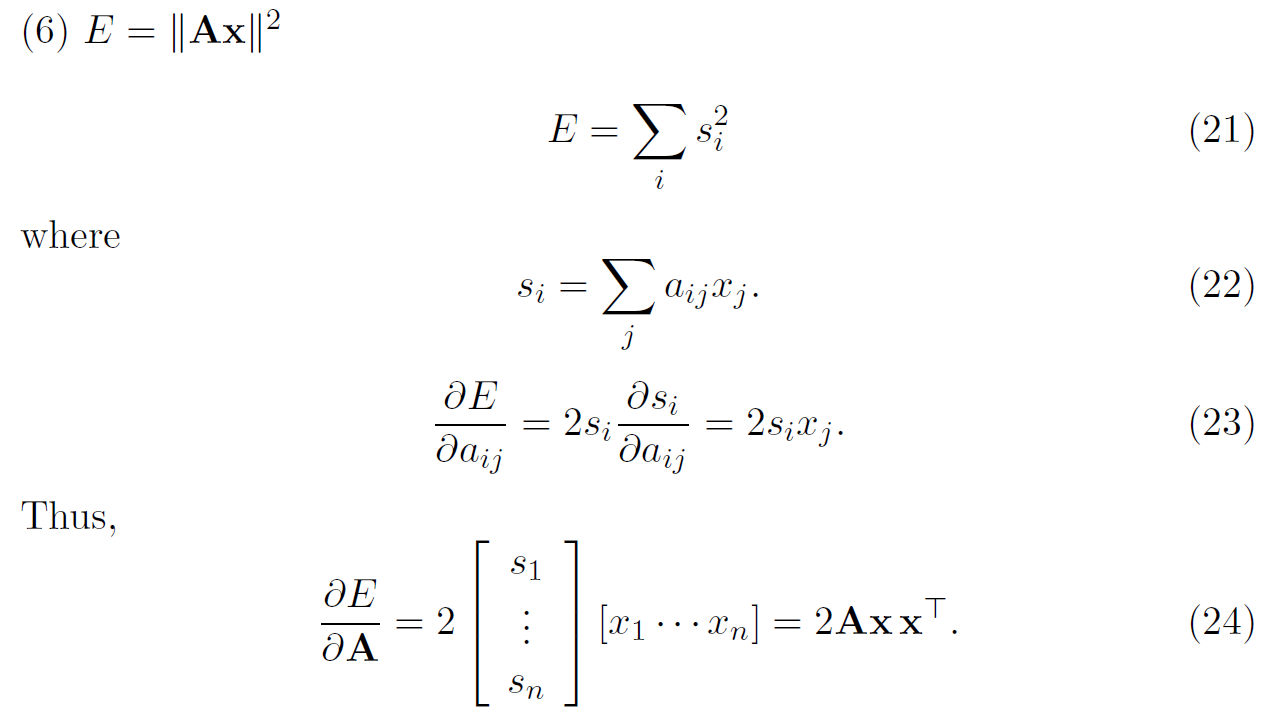
含trace的矩阵微分
矩阵迹是矩阵对角线的加和,可以用来定义矩阵的frobenius范数,所以常常出现在优化问题中。矩阵的Frobenius范数定义如下:
\[ ||\mathbf{A}||_F=(tr(\mathbf{A}\mathbf{A}^T))^{\frac{1}{2}} \]
对于\(\mathbf{A}\in\mathbb{R}^{n\times n}\),有等式如下:
\[ \mathbf{A}\mathbf{A}^T=\Sigma_{i=1}^n\mathbf{a}_i\mathbf{a}_i^T \]
即\(\mathbf{A}\mathbf{A}^T\)的结果是由每个列向量的自乘积相加产生的,同时我们可以观察到:
\[ (\mathbf{A}\mathbf{A}^T)_{ij}=\Sigma_{p=1}^na_{pi}a_{pj} \]
下面我们来观察线性函数\(\mathbf{x}^T\mathbf{Ax}\)的梯度,\(\mathbf{A}\in\mathbb{R}^{m\times n},\mathbf{x}\in\mathbb{R}^{n\times 1}\),我们有:
\[ \mathbf{x}^T\mathbf{Ax} = \mathbf{x}^T[\tilde{a}_1\mathbf{x},\cdots,\tilde{a}_n\mathbf{x}]^T=x_1\tilde{a}_1\mathbf{x}+\cdots+x_n\tilde{a}_n\mathbf{x} \]
那么有:
\[ \frac{\partial \mathbf{x}^T\mathbf{Ax}}{\partial x_k} = \Sigma_{i=1}^nx_ia_{ik}+\tilde{a}_k^T=\mathbf{a}_k^T\mathbf{x}+\tilde{\mathbf{a}}^T_kx \]
所以有\(\nabla_x \mathbf{x}^T\mathbf{A}\mathbf{x}=\mathbf{A}\mathbf{x}+\mathbf{A}^T\mathbf{x}\).
现在考虑\(E=tr(\mathbf{AX})\)对\(\mathbf{X}\)的求导,有\(tr(\mathbf{A(X}+d\mathbf{X}))=tr(\mathbf{AX})+tr(\mathbf{A}d\mathbf{X})\),因此我们只要考虑\(\frac{tr(\mathbf{A}d\mathbf{X})}{d\mathbf{X}}\)即可。

为了能够对矩阵范数中的矩阵求导,我们考虑\(E=tr(\mathbf{AB})\)对\(\mathbf{A}\)的导数:
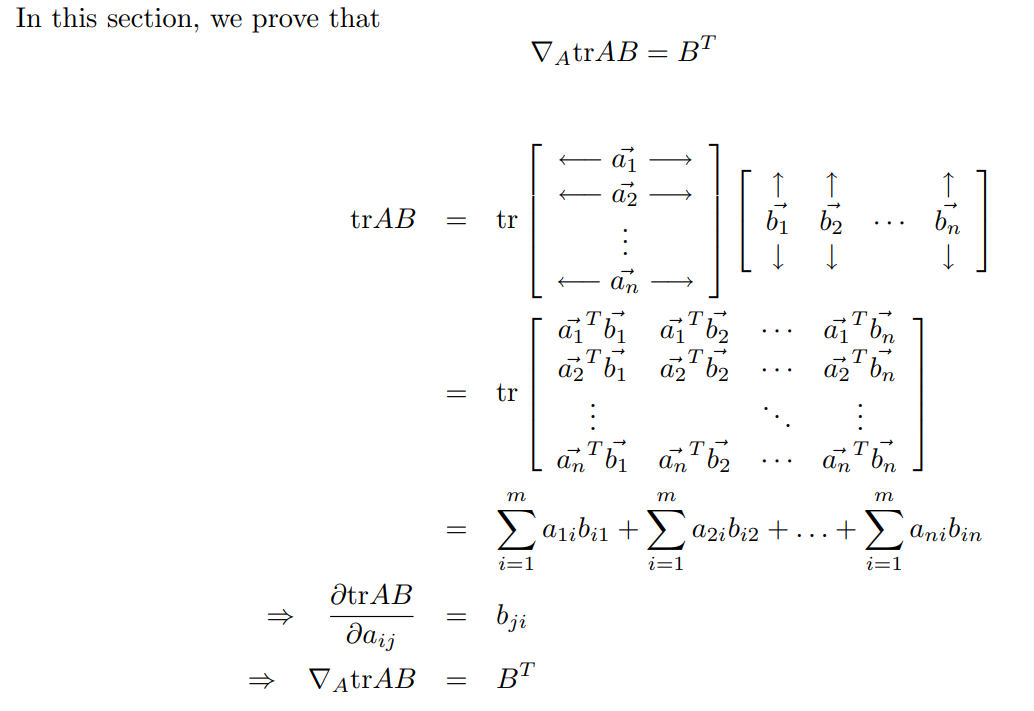
以及矩阵转置和矩阵微分的关系如下:
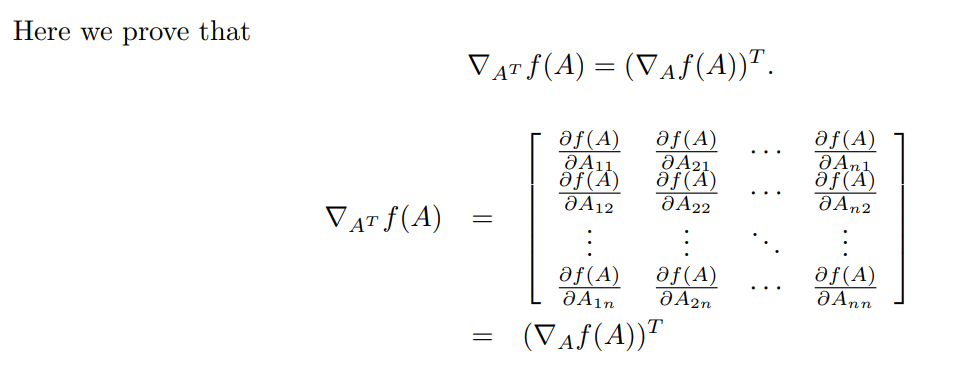
我们再考虑更一般的情况,假设\(f:\mathbb{R}^n\to\mathbb{R}\),\(\mathbf{A}\in\mathbb{R}^{n\times m}\),\(\mathbf{x}\in\mathbb{R}^{m\times 1}\),我们希望计算\(\nabla_x f(\mathbf{Ax})\). 根据链式法则:
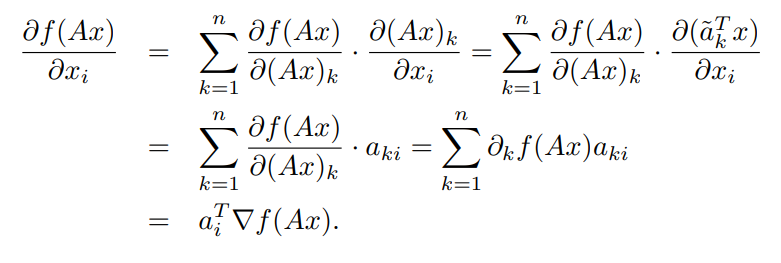
因此,有\(\nabla_x f(\mathbf{Ax})=\mathbf{A}^T\nabla f(\mathbf{Ax})\).
最后,我们考虑一个更复杂的例子,并展示链式法则是如何应用的:
\[ \nabla_\mathbf{A}tr(\mathbf{ABA}^T\mathbf{C})=\mathbf{CAB}+\mathbf{C}^T\mathbf{A}\mathbf{B}^T \]
令\(\mathbf{AB}=f(\mathbf{A})\),\(f\)为矩阵值函数: