这篇文章大部分理论贡献都来自其它文章,刻画了目前GNN对于同构判定的能力边界,总结得很好可以当综述看。这篇文章还提出了一个改进模型,能够在保持scalability的同时,在理论和实践上都更加优越:原文链接。
动机和贡献
- 目前的模型大多都不比1-WL test更强,因此表示能力非常有限。
- 能够达到2-WL test或者3-WL test的模型在复杂度上又很高。
因此,这篇文章提出了新的图卷积方式,有如下的特点:
- 仅在局部更新。
- 线性的时间、空间复杂度。
- 在理论和实践上都强于1-WL test。
对Weisfeiler-Lehman测试的刻画
这一章节的理论基本上都来自于别的工作,但是对于理解GNN的表示能力很重要。首先,我们介绍一下WL测试。
WL测试将图转化成为一个间接的形式,如果两个图的转换后形式不同,那么他们一定不是同构的(给出了同构的必要条件)。在第i次迭代时,每个节点都会被分配一个元组\(L_{i,n}\),包含节点老的压缩标签,以及所有邻居的压缩标签。每次迭代中,都会对节点分配一个压缩标签,两个拥有相同\(L_{i,n}\)的节点会得到相同的压缩标签。
- 初始化,对每个节点\(n\)分配标签\(C_{0,n}=1\)
- 在第\(i\)次迭代中,对于节点\(n\),设置\(L_{i,n}\)为一个元组包含旧标签\(C_{i-1,n}\)以及所有邻居\(C_{i-1,m}\)的可重复集合。
- 得到\(L_{i,n}\)进行hash,得到\(C_{i,n}\)
- 根据压缩标签去划分节点。重复2和3共\(N\)次(总节点数),或者直到迭代不会改变节点划分。
这上面的算法叫做1-WL测试,也叫节点涂色。在初始阶段,所有节点都被涂成相同的颜色\(H_v^{(0)}=1\)。然后颜色按照下面的规则更新: \[ H_v^{(t+1)}=\sigma(H_v^{(t)}|\{H_u^{(t)}:u\in\mathcal{N}(v)\}), \] 高阶的WL测试基本上是相似的,但更新方式有一些不同。2-WL测试使用二阶节点元组,即所有节点对的排列,因此需要\(\mathbf{H}\in\mathbb{R}^{n\times n}\)矩阵。初始阶段有额外的两种颜色:
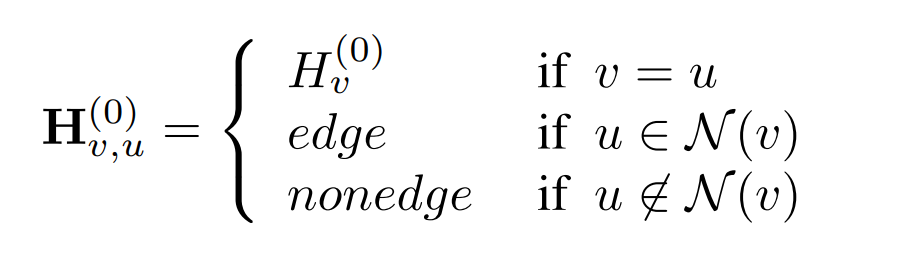
然后按照如下的方式进行更新: \[ \mathbf{H}_{v,u}^{(t+1)}=\sigma(\mathbf{H}_{v,u}^{(t)}|\{\mathbf{H}_{v,k}^{(t)}:k\in[n]\}|\mathbf{H}_{k,u}^{(t)}:k\in[n]|) \] 但根据最近的结果Provably powerful graph networks,2-WL测试并不比1-WL更有效。只有\(k\ge 2\)时,(k+1)-WL测试才比k-WL更有效。他们进一步提出了Folkore WL测试,1-WL=1-FWL测试,但是当\(k\ge 2\)时,(k+1)-WL测试约等于\(k\)-FWL测试。2-FWL测试的迭代方式如下: \[ \mathbf{H}_{v,u}^{(t+1)}=\sigma(\mathbf{H}_{v,u}^{(t)}|\{(\mathbf{H}_{v,k}^{(t)}|\mathbf{H}_{k,u}^{(t)}):k\in[n]\}) \] 另外的一项研究MATLANG,则将矩阵运算与WL测试关联起来,用更清晰的方式刻画了WL测试的判别能力。同时由于神经网络就是基于矩阵运算,MATLANG实际上也刻画了GNN的判别能力。我们首先给出两个定义:
定义1. \(ML(\mathcal{L})\)由一系列矩阵运算构成,\(\mathcal{L}\)限定了运算的种类,比如\(\mathcal{L}=\{.,+,\operatorname{diag},\operatorname{tr},\times\}\)
定义2. \(e(X)\in\mathbb{R}\)是\(ML(\mathcal{L})\)中的一个句子,它指定了顺序执行的一系列矩阵操作,并产生一个标量值。
举个例子,\(e(X)=\mathbf{1}^TX^2\mathbf{1}\)就是\(\mathcal{L}=\{.,^T,\mathbf{1}\}\)中的一个句子。下面给出了与1-WL,2-WL,3-WL测试等价的三个matlang:
- \(\mathcal{L}_1=\{.,^T,\mathbf{1},\operatorname{diag}\}\)产生的\(ML(\mathcal{L}_1)\)和1-WL测试是等价的。
- \(\mathcal{L}_2=\{.,^T,\mathbf{1},\operatorname{diag},\operatorname{tr}\}\)产生的\(ML(\mathcal{L}_2)\)比1-WL测试更强,但是比3-WL测试弱。
- \(\mathcal{L}_3=\{.,^T,\mathbf{1},\operatorname{diag},\operatorname{tr},\odot\}\)产生的\(ML(\mathcal{L}_3)\)和3-WL测试是等价的。
- 对上面的三个运算集增加\(\{+,\times,f\}\)不会提升判定能力,记为\(\mathcal{L}^{+}\)。
MPNN的能力
这一章节总结了现有的一些结果,对MPGNN的判定能力做了很好的刻画。
定理1. MPNN如GCN,GAT,GraphSage,GIN都不比1-WL测试更有效
Chebnet也被证实不比1-WL测试更有效,但是只有当两张图的最大特征值相同的时候成立,当两者有差别时,Chennet是强于1-WL测试的。
定理2. 如果两张图laplacian的最大特征值不同,那么Chebnet是比1-WL测试强的。下面这张图给出了一个例子。
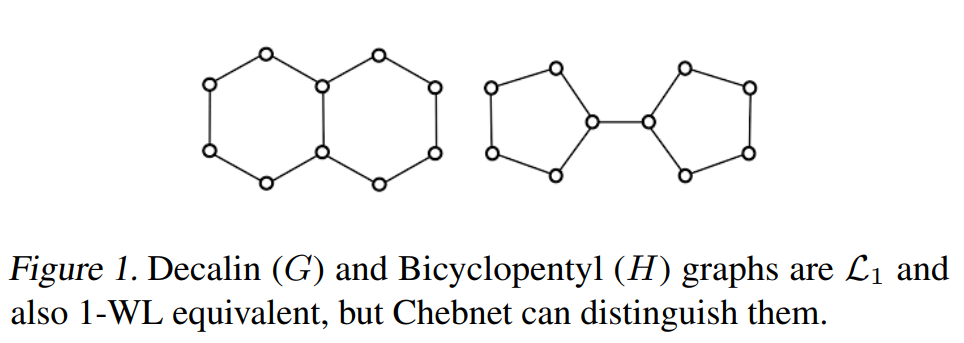
除了判定同构图以外,GNNs同时也应该具备统计子结构的能力,下面的定理刻画了MATLANG的计数能力。
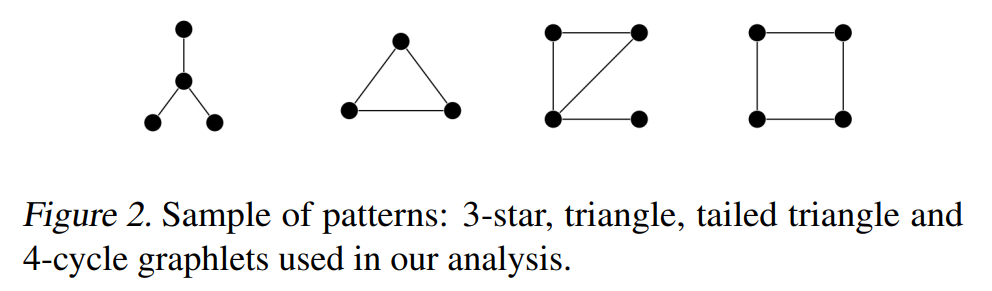
对于上面的四种结构,我们有如下的定理:
定理3. \(\mathcal{L_1^{+}}\)可以准确统计3-star的个数。
定理4.\(\mathcal{L_2^{+}}\)可以准确统计triangle和4-cycle的个数。
定理5.\(\mathcal{L_3^{+}}\)可以准确统计Tailed triangle的个数
上面这些定理说明1-WL等价的MPNN只能对3-star计数,而3-WL等价的MPNN可以对上面所有子图计数。
另一方面Dehmamy表明,MPNN如果没有合适的卷积核,无法学习到节点度数。因此,这里假定节点度数本身包含在节点特征向量中。然而,可以证明3-star的总数可以由节点度数得到。因此只要提供了节点度数,简单的MLP就可以统计3-star的数量。
强于1-WL测试的MPNN
提出了两个MPNN模型,一个是GNNML1,另一个是GNNML3。前者和1-WL测试等价,后者比1-WL更强,可以在实验中和3-WL测试接近。GNNML1的更新规则如下:
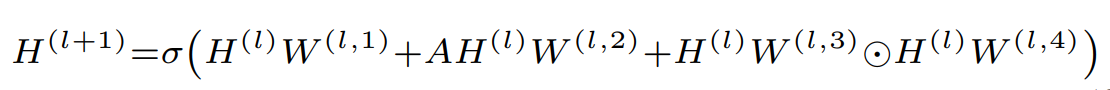
\(W^{(l,s)}\)是可学习的参数,它包含三个部分,整体很简单。它的表示能力由如下的定理刻画:
定理6.GNNML1可以产生\(ML(\mathcal{L_1})\)中所有可能的句子,因此GNNML1和1-WL测试是等价的。
根据之前的结果,想要达到3-WL测试的能力,还需要\(\operatorname{tr}\)操作。我们回到Figure 1,可以容易得到左边邻接矩阵五次幂的trace为0,而右边邻接矩阵五次幂的trace是20. \(tr(A^5)\)实际上给出了长度5的闭环路径的数量。
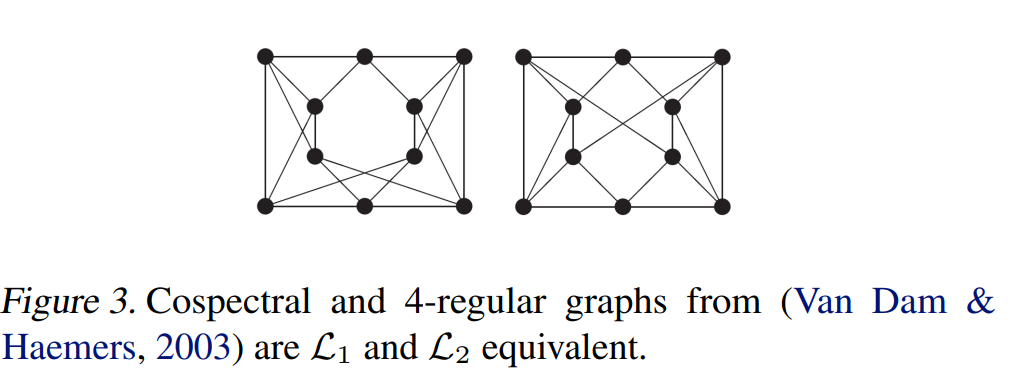
尽管trace可以让我们表示更复杂的性质,但对于Figure3中的cospectral图是没有用的,它们总是拥有相同的闭环路径数量。在这种情况下,逐元素乘积是必要的。比如,\(e(A)=\mathbf{1}^Tf((A\odot A^2)^2\mathbf{1})\),\(f(x)=x\odot x\)这个句子,左边的输出是6032,右边的输出则是5872.
可以观察到,上面的操作中涉及到了矩阵的幂次,但是为了保持效率,MPNN实际上不会显式地计算矩阵次幂。因此对矩阵次幂取trace也是不可能的。
为了解决这个问题,一个方式是使用MASK去保证稀疏性,即\(C^{(s)}=M\odot A^s\),比如可以取\(M=A+I\),它可以保持前后稀疏度相同。尽管没办法计算所有可能矩阵的逐元素乘积,但是可以产生所有\((M\odot A^s)^l\)形式的句子,\(l\in[0,l_{max}]\),\(l_{max}\)是模型层数,\(s\in[0,s_{max}]\)是预计算的矩阵幂。本文最终模型中实际上用的是矩阵分解的形式,我们来看一看算法的伪代码。


我感觉看看就好,肯定不太实用。
数据集
他们使用的数据集可以用在别的evaluation上,了解一下:
- graph8c和sr25Graph8c包含11117种可能的8节点图,那么就有超过61M个对,其中有312对是1-WL等价的,但是没有3-WL等价的对。sr25包含25节点构成的图,并且每个节点的度数都是12,连接节点共享5个常见领域,非连接节点包含6个常见领域。Sr25总共有15张graph,有105个pair.
- EXP,EXP包含600对1-WL等价的图。同时数据集还包含一个二分类任务,每一对中的两个图都被分到不同的类。
高低通滤波器检验:根据Balcilar的分析,现有的MPNN大多都是低通滤波器。本文使用了他们提出的数据集来验证模型是否只能学习到低通滤波器的行为。根据结果来看,Chebnet实际上已经和GNNML3差不多了。
最后是两个benchmark数据集Zinc12K和MNIST-75,前者需要基于结构信息,而后者基于图像分析,需要模型能够处理谱域信息。
结语
总的来说文章的方法的性能是不错的,但是并没有超出现有方法很多。这篇文章的价值在于对目前MPNN的能力进行总结,实验的结果也和理论能够对上。