SSL on Graphs Insights and New Directions

Self-supervised Learning on Graphs: Deep Insights and New Directions

最近想搞一篇关于自监督图学习的工作，之前博客有一篇基于Transformer的。但这个工作太暴力了，效果也非常的好，比肯定很难比得过，所以不可能再去做这个领域（好在它只是做分子数据的）。

Abstract

利用自监督学习（SSL）来利用Graph中未标注数据。这篇工作研究了几个基础的SSL任务：它们什么时候对图神经网络（GNNs）有用。基于经验性的研究，这篇工作提出一个新的方向selftext，它可以在多个现实场景数据达到最佳性能。代码链接

Introduction

首先SSL在图像和文本领域已经有很大成效。它通过设计domain-specific辅助任务来为无标签数据引入伪标签，这使得模型从这些辅助任务中学习到有益于下游任务的数据表示。

其次GNNs在图的表示学习中非常强大，多种任务都可以由它完成比如节点分类、图分类。这篇工作聚焦于半监督的节点分类任务，这个任务使用了标注/未标注节点来学习节点表示，并得到一个对未标注节点进行分类的分类器。一方面，GNNs从设计上就是自然支持半监督的。另一方面，这种半监督仅仅是基于特征聚合层面上的。

后面又说明了图数据本身的复杂性。图数据不仅考虑个体（个体可以是用户的信息、也可以是一张图片、一段文本等等），更重要的还考虑了这些个体之间的关系。进一步说，只要拥有这种关系描述，任何数据集都可以当成图数据集来理解。如果不能较好的利用这种关系，其它领域的方法就不能在图数据集上达到好的效果。这种复杂性也为高级的自监督辅助任务设计提供了可能。最近开始有一些对图SSL领域的探索性工作，还处于初步阶段。

这篇工作基于两个目标来开展节点分类的图SSL研究：1.那些SSL任务对GNNs有用。2.图领域新的SSL研究方向。对第一个目标，作者基于attribute和结构信息设计了一些基础的自监督任务，并用实验探究了他们的效果。对第二个目标，作者提出了一个selftask，达到了SOTA性能。

Problem Statement

图分成两部分，节点和边，边就是邻接矩阵\(A\)，节点则拥有一个特征向量，描述了该节点的特性（所有节点的特征向量构成特征向量矩阵\(X\)）。同时\(D_L=(V_L,Y_L)\)代表有标签数据，\(D_U\)代表未标注数据。\(f_\theta:V_L\to Y_L\)是图神经网络，将节点分到特定类别。对应的优化问题如下： \[ \min_{\theta}L_{task}(\theta,A,X,D_L)=\Sigma_{(v_i,y_i)\in D_L}l(f_\theta(\mathcal{G})_{v_i},y_i), \] 沿用这些符号，我们定义图SSL如下：

Problem1 给定一个数据集\(\mathcal{G}=(A,X)\)，以及标注数据\(D_L=(V_L,Y_L)\)。目标是构造一个自监督辅助任务，并有一个对应损失\(L_{self}\)，可以与\(L_{task}\)结合得到对未标注数据性能更好的\(f_\theta\)。

Basic Pretext Tasks on Graphs

有两个设计任务的方向，1.underlying图结构信息。2.节点特征信息。这里作者讨论了几个很直接的任务设计。

Structure Information

基于局部结构信息来为未标注数据构造标签，或者基于它们如何与图其余部分关联。

Local Structure Information

NodeProperty. 在这个任务中，我们让模型预测节点的度数、局部重要性、局部聚类系数。在本工作中，作者使用度数作为标签。令\(d_i=\Sigma_{j=1}^NA_{i,j}\)，然后定义如下的损失： \[ L_{self}(\theta',A,X,D_v)=\frac{1}{|D_U|}\Sigma_{v_i\in D_U}(f_{\theta'}(\mathcal{G})_{v_i}-d_i)^2 \] Remark 显然，这个任务是一个非常trivial的任务，我觉得不会带来多大提升。

EdgeMask. 随机mask一些边，然后让模型重构这些边。首先mask\(m_e\)条边，令\(M_e\subset\mathcal{E}\)，同时采样一个无边集合\(\bar{M_e}=\{(v_i,v_j)|v_i,v_j\in V and (v_i,v_j)\notin\mathcal{E}\}\)，\(|M_e|=|\bar{M}_e|=m_e\)，该任务定义损失如下： \[ \begin{aligned} L_{self}(\theta',A,X,D_U)&=\frac{1}{|M_e|}\Sigma_{(v_i,v_j)\in M_e}l(f_w(|f_{\theta'}(\mathcal{G})_{v_i}-f_{\theta'}(\mathcal{G})_{v_j}|),1)\\ &+\frac{1}{|\bar{M}_e|}\Sigma_{(v_i,v_j)\in \bar{M}_e}l(f_w(|f_{\theta'}(\mathcal{G})_{v_i}-f_{\theta'}(\mathcal{G})_{v_j}|),0) \end{aligned} \] Remark 这个任务的设计是比较好的，增加了一个link prediction的任务，直接让节点表示学习到节点间的相关性。唯一担心的是这个监督会不会过强。

Global Structure Information

全局的自监督任务不限于单个节点或者一阶邻域，并且会关注节点在整个图中的位置。

PairwiseDistance. 该任务预测节点对之间的距离。这个距离可以由很多方式定义，比如是否属于同一个连通子图，personalized PageRank或者其它可以计算节点相似性的全局link prediction。在这篇工作中，使用的是最小路径长度作为两个节点的距离度量。首先为所有节点计算最短路径，然后将节点对分为四个类别：\(p_{ij}=1,p_{ij}=2,p_{ij}=3,p_{ij}\ge 4\)。此外，为了减少计算量，这个过程也是由采样完成的。随机抽取节点对集合\(\mathcal{S}\)，然后构造多类别分类损失如下： \[ L_{self}(\theta',A,X,D_U)=\frac{1}{|\mathcal{S}|}\Sigma_{(v_i,v_j)\in\mathcal{S}}l(f_w(|f_{\theta'}(\mathcal{G})_{v_i}-f_{\theta'}(\mathcal{G})_{v_j}|),C_{p_{ij}}) \] 这里\(C_{p_{ij}}\)对应节点对\(p_{i,j}\)所属的类别。

Remark这个任务接近于上面的linkprediction，并且比上面的任务更强一些。所以在消融时两个任务的效益肯定是很大相关的，消融实验时区别也不会很大。

Distance2Clusters.前一个任务计算量非常大，为了更容易获得标签，这个任务转而预测节点距锚节点集合的距离。首先，它使用METIS将图切割为\(k\)个簇\(\{C_1,C_2,\dots,C_k\}\)。对每个簇，该任务将度数最大的节点作为中心\(c_j\)。这样，对每个节点\(v_i\)都可以构成一个向量\(d_i\in\mathbb{R}^k\)，\(d_i\)的第j个元素就是\(v_i\)和\(c_j\)的距离。对应的损失为： \[ L_{self}(\theta',A,X,D_U)=\frac{1}{|D_U|}\Sigma_{v_i\in D_U}||f_{\theta'}(\mathcal{G})_{v_i}-d_i||^2 \] Remark 对于在簇边缘的点，\(d_i\)将变得失去意义。

Attribute Information

这部分的任务更类似于传统图像/文本领域的SSL，关注于实例本身的特征。

AttributeMask.随机掩码一部分Attribute，然后要求GCNs去重建这些特征。

PairwiseAttrSim. 令\(T_s,T_d\)为最相似/不相似节点对： \[ T_s=\{(v_i,v_j)|s_{ij}\text{ in top-K of }\{s_{ik}\}_{k=1}^N\backslash\{s_{ii}\},\forall v_i\in V_U\}\\ T_s=\{(v_i,v_j)|s_{ij}\text{ in bottom-K of }\{s_{ik}\}_{k=1}^N\backslash\{s_{ii}\},\forall v_i\in V_U\} \] \(s_{ij}\)为\(v_i,v_j\)节点特征间的余弦相似度，\(K\)为参数。随后可以定义一个如下的回归任务： \[ L_{self}(\theta',A,X,D_U)=\frac{1}{|T|}\Sigma_{(v_i,v_j)\in T}||f_w(|f_{\theta'}(\mathcal{G})_{v_i}-f_{\theta'}(\mathcal{G})_{v_j}|)-s_{ij}||^2 \] 这里\(T=T_s\cup T_d\)，即只做最相似/不相似部分节点的预测。

Remark 感觉没啥用的任务

Preliminary Analysis

GSSL

TwoStage

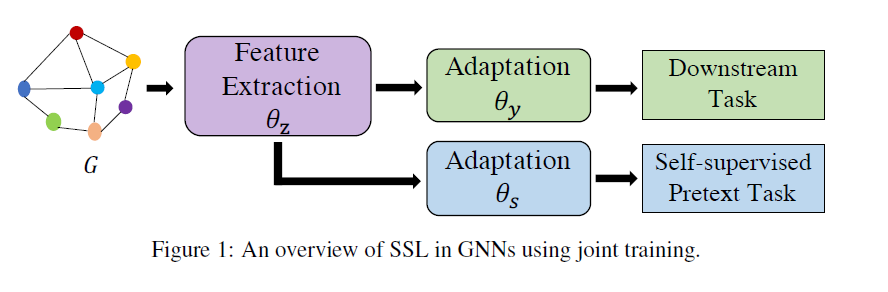
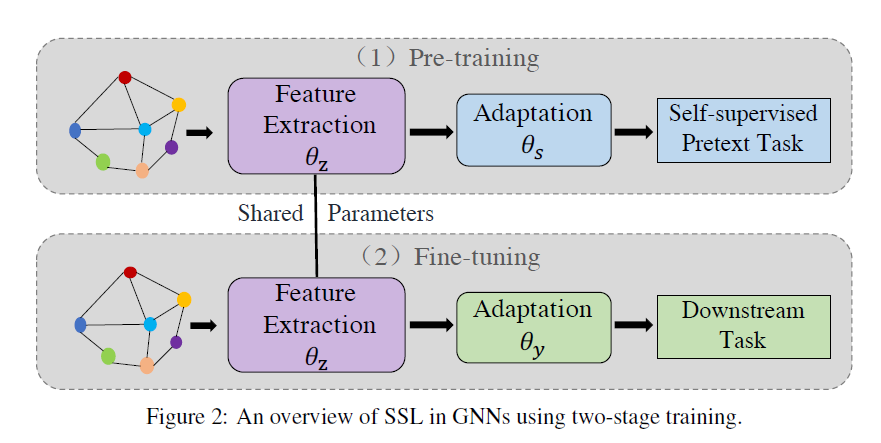
对于图上的自监督学习，Figure1展示了其模型结构。一部分参数用于完成自监督任务，这部分参数并不参与下游任务；另一部直接参与了表示学习的过程，在下游任务中会发挥作用。FIgure2则展示了常见的两阶段策略，在第一阶段进行自监督的预训练，第二阶段使用标注数据对模型进行微调以适配下游任务。

Emprical Study

Result1

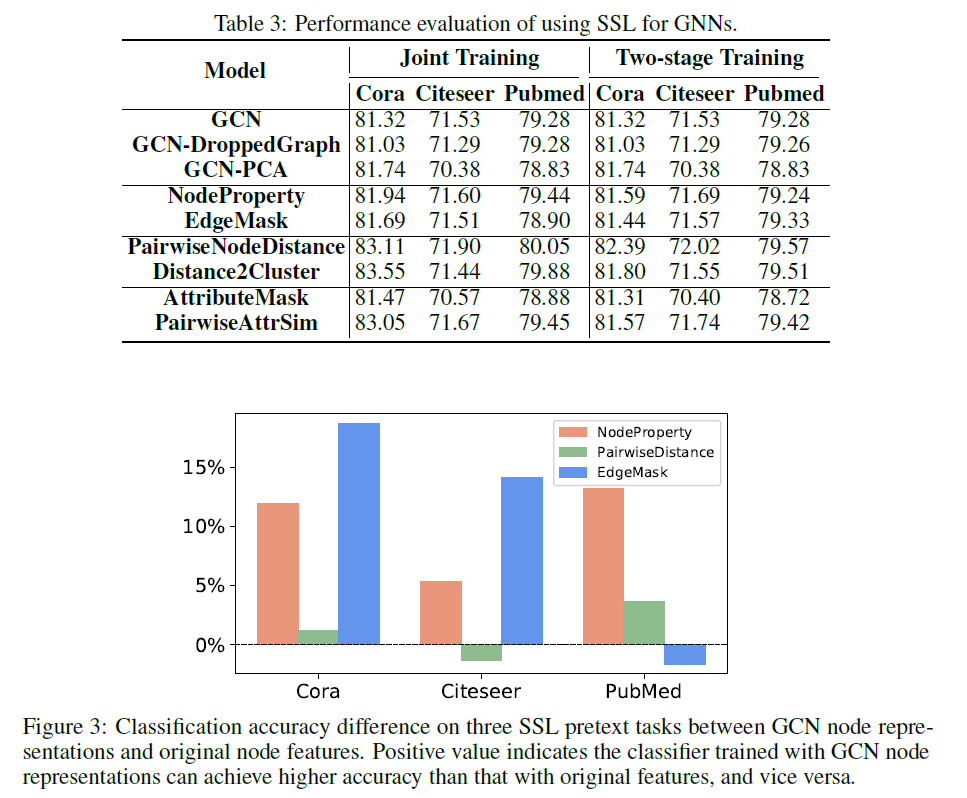
可以看到PairwiseNodeDistance,Distance2Cluster,PairwiseAttrSim这三个任务对Cora数据集是有效的，对其它两个数据则没什么帮助，整体上这些自监督任务提升都非常有限。个人认为跟模型的capability有关系，换成类Transformer的模型会好一点。另一方面，这些任务设计上肯定是有欠缺的，没有什么作用。

Advanced Pretext Tasks on Graphs

提出了SelfTask. 我感觉这个称不上是自监督，因为是依赖于已有的标签的，顶多算半监督。自监督应当胜任大规模的跨数据集无监督训练。

SelfTask: Distance2Labeled

相比之前的Distance2Cluster（用METIS分割图的那个），只是将类别换为到\(c_j\)的最长路径、最短路径、平均路径，构成一个\(3K\)的向量（\(K\)为簇中心数量）。

SelfTask: ContextLabel

用一个基于相似的函数，能够基于结构、特征、以及当前已标注的节点来提供一个邻域标签分布语义向量\(\bar{y}_i\)： \[ f_s(A,X,D_L,V_U)\to\{\bar{y}_i|v_i\in V_U\} \] 作者用\(k\)阶邻域的节点来定义这个语义向量： \[ \bar{y}_{ic}=\frac{|N_{V_L}(v_i,c)|+|N_{V_U}(v_i,c)|}{|N_{V_L}(v_i)|+|N_{V_U}(v_i)|},c=1,\dots,K \] \(N_{V_U}(v_i)\)代表\(v_i\)邻域中属于\(V_U\)的节点，\(N_{V_U}(v_i,c)\)代表其中属于\(c\)的节点。得到语义向量后就可以定义一个回归任务。很多方法都可以将已有的标签扩展到未标注节点上，比如Label Progation(LP)和Iterative Classifciation Algorithm(ICA)。这样得到的标签很弱，也有很多噪声。

SelfTask: EnsembelLabel

通过ContextLabel以及不同的标签传播算法，可以得到不同的\(f_s\)。假定\(v_i\)被LP和ICA对应的\(f_s\)决定的类别概率为\(\sigma_{LP}(v_i)\)和\(\sigma_{ICA}(v_i)\)，则选择\(\bar{y}_i\)为： \[ \bar{y}_i=\arg\max_c \sigma_{LP}(v_i)+\sigma_{ICA}(v_i),c=1,\cdots,K \] 即最一致的类别。

SelfTask: CorrectedLabel

简要说一下流程。分为训练和纠正两个阶段：在训练阶段，使用纠正标签去构建纠正语义标签分布向量，然后利用原始/纠正语义向量进行训练，纠正语义向量的回归损失权重为\(\alpha\)。

在纠正阶段，用GCN为每个类别\(c\)选择\(p\)个类别原型\(\{z_{c1},\dots,z_{cp}\}\)。先随机采样\(m\)个同样类的节点，然后计算它们的嵌入相似矩阵\(S\)。定义密度如下： \[ \rho_i=\Sigma_{j=1}^m\operatorname{sign}(S_{ij}-S_c) \] \(S_c\)是一个定值，作者将其定为前40%的分位数。较小的\(\rho\)代表该节点与其它同类节点相似度比较低，作者选择\(\rho\)前\(p\)个节点作为类原型（因为它们一致性更高）。然后计算一个纠正标签如下： \[ \hat{y}_i=\arg\max_c\frac{1}{p}\Sigma_{l=1}^p\operatorname{cos}(f_{\theta'}(\mathcal{G})_{v_i},z_{cl}),c=1,\dots,K \] 即看节点跟那些类原型更相似，\(\operatorname{cos}(\cdot,\cdot)\)是余弦相似度。通过这样的两阶段迭代，模型能逐渐提升标签的准确性。

Experiments

Selftask

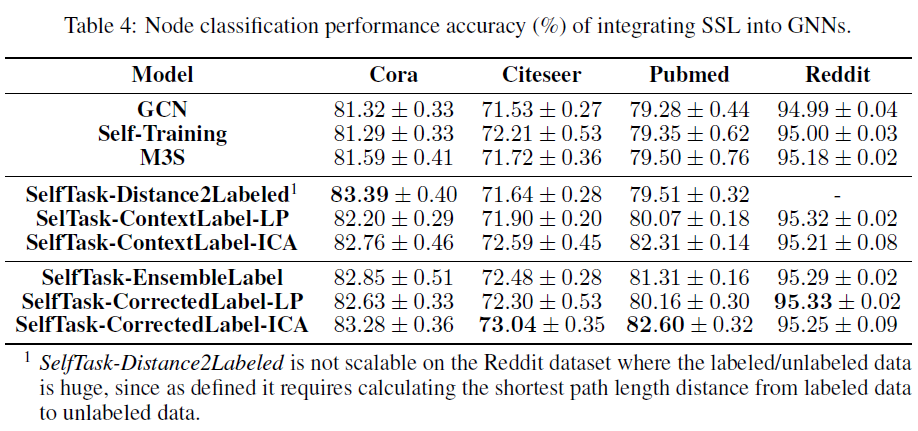
之前在cora上pairwiseattrsim可以到83.05的精度，在Citeseer上pairwisenodedistance有72.02的精度，在Pubmed上pairwisenodedistance有80.05的精度。这样看起来selftask的几个任务都是比较有效的，尤其是最后一种。但是在Reddit上提升一般，可能对大数据集没有什么用处。

Analysis

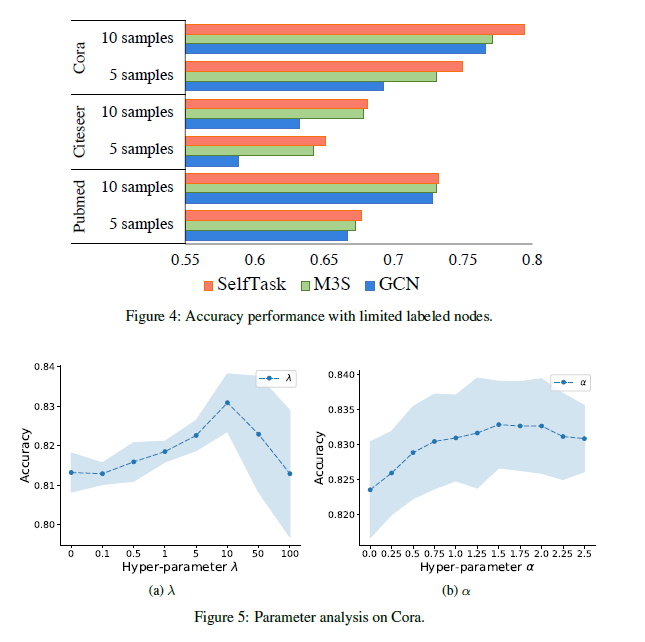
Figure4讨论了标签极少的情况，即每类只有5/10个样本，可以看到SelfTask在三个数据集上仍然有效。\(\lambda,\alpha\)分别是自监督任务的权重以及correctedlabel中纠正标签的权重。Figure5说明了自监督任务的重要性，以及纠正标签的有效性。

结论

这篇工作首先研究了几个naive的自监督的效果，这些自监督任务整体上都没有什么特别大的用处，给我们设计自监督任务一些启示。首先将点和边分离地看待是不行的，单独为两个部分设计任务意义并不大，一些更注重邻域语义的任务才是有效的。这篇文章提出的SelfTask非常奇怪，和前文那些任务衔接不够好，并且还是基于已有标签的，无法用于大规模的无监督预训练。并且最有效的那个任务还是偷来的，没有很大价值。这篇文章跟Self-Supervised Graph Transformer on Large-Scale Molecular Data这篇文章对比着看才显得有价值，给了我们一些失败经验。

一些构思

目前来说，基于对比的思路更吃香一点（在图像和文本领域）。Self-Supervised Graph Transformer on Large-Scale Molecular Data告诉我们，抽取graph的样式来编码邻域是很有用的，按照节点对的类型来编码邻域也有用。总的来说，我们必须关注节点所处位置的语义信息（相对于数阶邻域）。另一方面，图中似乎欠缺一种顺序关系：邻域中的各个节点并没有一个给定的次序。我想知道这种次序是否对编码邻域有意义，以及对比的思路（基于随机掩码节点/边）是否有效。大致是这两条路线。